De middeleeuwse wiskundige Leonardo Fibonacci's probleem over konijnen

Laten we eens kijken hoe het aantal konijnen in de eerste zes maanden groeit:

Maand 1. Een paar jonge konijnen.

Maand 2. Er is nog één origineel paar. Konijnen hebben de vruchtbare leeftijd nog niet bereikt.

Maand 3. Twee paar: de originele, die de vruchtbare leeftijd heeft bereikt + het paar jonge konijnen dat ze heeft gebaard.

Maand 4. Drie paar: een origineel paar + een paar konijnen die ze aan het begin van de maand heeft gebaard + een paar konijnen die in de derde maand zijn geboren, maar nog niet geslachtsrijp zijn.

Maand 5. Vijf paar: één origineel paar + één paar geboren in de derde maand en vruchtbare leeftijd bereikt + twee nieuw paren van wie ze zijn bevallen + een paar dat in de vierde maand is geboren, maar nog niet is bereikt volwassenheid.

Maand 6. Acht koppels: vijf koppels van vorige maand + drie pasgeboren koppels. Enzovoort.

Laten we, om het duidelijker te maken, de ontvangen gegevens in de tabel schrijven:

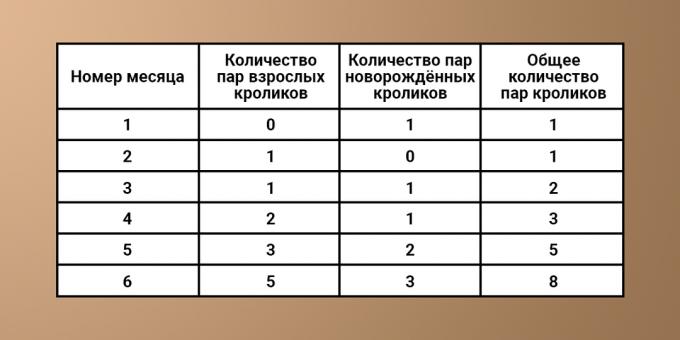
Als u de tafel zorgvuldig bestudeert, kunt u het volgende patroon herkennen. Elke keer is het aantal konijnen dat in de nde maand aanwezig is gelijk aan het aantal konijnen in de (n - 1) de vorige maand, opgeteld bij het aantal pas geboren konijnen. Hun aantal is op zijn beurt gelijk aan het totale aantal dieren vanaf de (n - 2) maand (die twee maanden geleden was). Hieruit kun je afleiden

formule:

F._n = F_{n - 1}+ F._{n - 2},

waar F_n - het totale aantal paren konijnen in de n-de maand, F_{n - 1} Is het totale aantal konijnenparen in de afgelopen maand, en F._{n - 2} - het totale aantal konijnenparen twee maanden geleden.

Laten we het aantal dieren in de volgende maanden tellen:

Maand 7. 8 + 5 = 13.

Maand 8. 13 + 8 = 21.

Maand 9. 21 + 13 = 34.

Maand 10. 34 +21 = 55.

Maand 11. 55 + 34 = 89.

Maand 12. 89 + 55 = 144.

Maand 13 (begin volgend jaar). 144 + 89 = 233.

Aan het begin van de 13e maand, dat wil zeggen aan het einde van het jaar, zullen we 233 paren konijnen hebben. Hiervan zullen 144 koppels volwassen zijn en 89 jong. De resulterende reeks 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233 genaamd Fibonacci-nummers. Daarin is elk nieuw definitief nummer gelijk aan som de vorige twee.